Định lý Pytago là gì? Công thức định lý Pytago và bài tập vận dụng?

Định lý Pytago trong tam giác vuông và các bài tập vận dụng

     Toán học đã và đang là một lĩnh vực rất quan trọng trong cuộc sống của chúng ta. Nó không chỉ giúp ta giải quyết các vấn đề phức tạp mà còn là một công cụ hữu ích để hiểu và giải thích những hiện tượng xảy ra trong thế giới xung quanh chúng ta. Trong những khái niệm cơ bản của toán học, định lý Pythagoras luôn là một trong những khái niệm được đánh giá cao và rất quan trọng. Hãy cùng bài viết sau tìm hiểu về định lý Pythagoras và vai trò của nó trong toán học và cuộc sống của chúng ta.

1. Nguồn gốc của định lý Pytago?

     Định lý Pythagoras được đặt theo tên của nhà toán học người Hy Lạp Pythagoras (khoảng 570 TCN - 495 TCN), người được cho là người đầu tiên phát hiện ra định lý này. Tuy nhiên, có nhiều ý kiến cho rằng định lý Pythagoras không phải do Pythagoras phát hiện ra mà là do những người khác trước đó đã biết đến định lý này.

     Trong thời kỳ cổ đại, những phương pháp đo lường độ dài thường dựa trên sự so sánh với các đơn vị đo lường khác nhau. Tuy nhiên, để tính toán chính xác các độ dài trong các bản vẽ và thiết kế, cần phải có các quy tắc và công thức hình học. Định lý Pythagoras đã trở thành một trong những công thức quan trọng nhất trong hình học và được áp dụng rộng rãi trong nhiều lĩnh vực khác nhau.

     Trong thời kỳ trung cổ, định lý Pythagoras đã được giới thiệu đến châu Âu qua các nhà toán học Ả Rập và được phổ biến rộng rãi trong thế giới phương Tây. Hiện nay, định lý Pythagoras vẫn là một trong những định lý cơ bản nhất trong toán học và được giảng dạy trong các trường học trên toàn thế giới.

2. Định lý Pytago và những ví dụ minh hoạ.

     Định lý Pytago là một định lý toán học cơ bản về các tam giác vuông. Nó khẳng định rằng trong một tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai cạnh kề.

     Cụ thể: Cho tam giác ABC vuông tại A, ta có thể suy ra:

BC² = AB² + AC²

     Trong đó:

     - AB và AC là độ dài của hai cạnh kề của tam giác vuông.
     - BC là độ dài của cạnh huyền của tam giác vuông.

     Các ví dụ minh hoạ: 

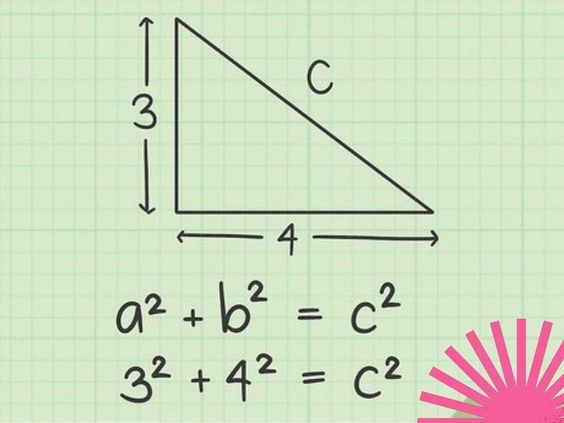
     Ví dụ 1: Tam giác ABC vuông tại A có AB = 3cm, AC = 4cm. Tính độ dài cạnh BC

     Theo định lý Pytago, ta có:

     BC² = AB² + AC² = 3² + 4²
     BC = 5 cm

     Do đó, độ dài của BC là 5 cm.

     Ví dụ 2: Tam giác ABC vuông tại A có BC = 5 cm và độ dài của AB = 3 cm. Bạn muốn tính độ dài của cạnh góc vuông còn lại.

     Theo định lý Pytago, ta có:

     BC² = AB² + AC² , Thay số vào ta được 5² = 3² + AC²

     25 = 9 +AC² nên AC² = 16

      AC= 4cm

     Do đó, độ dài của cạnh góc vuông còn lại AC là 4 cm.

     Định lý Pytago đảo

     Cho tam giác ABC có ba cạnh AB,AC và BC. Nếu  AB² + AC² = BC²   Suy ra tam giác ABC là tam giác vuông tại A

     Ví dụ 3: Cho tam giác ABC có AB=5, AC = 12 , BC=13 Chứng minh tam giác ABC vuông tại A

     Áp dụng Pytago đảo ta có :  5² + 13² = 13² 

     mặt khác BC có độ dài là 13cm là cạnh lớn nhất nên BC là cạnh huyền của tam giác

     Suy ra tam giác ABC vuông tại A

3. Một số bài tập vận dụng liên quan đến định lý pytago.

     3.1. Giả sử bạn muốn xây dựng một tấm bảng dài 6m và cao 8m có đường chéo dài bao nhiêu?

     Lời Giải

     - a là chiều dài tấm bảng

     - b là chiều cao tấm bảng

     - c là đường chéo tấm bảng

     Theo định lý Pytago, ta có:

     c² = a² + b², thay số ta có c² = 6² + 8²
     Vậy c² = 100 nên c = 10m

     Do đó, đường chéo của tấm bảng là 10m

3.2. Xây dựng một vườn hình vuông với diện tích 25 m². Tính độ dài cạnh của vườn.

     Theo định lý Pytago, ta có: c² = a² + b²

     Trong trường hợp này, a = b vì đó là một vườn hình vuông, và diện tích của vườn là 25 m².

     a² = b² = 25 / 2

     a = b = √(25 / 2)

     a = b ≈ 3.54 m

     Do đó, độ dài cạnh của vườn hình vuông là khoảng 3,54 mét.

3.3. Giả sử bạn muốn tính độ dài của một cáp treo giữa hai điểm cao nhất trên hai ngọn núi. Bạn biết khoảng cách ngang giữa hai ngọn núi là 400 m và độ cao của mỗi ngọn núi là 300 m. Bạn muốn biết độ dài của cáp treo.

     Theo định lý Pytago, ta có: c² = a² + b²

     Trong trường hợp này, a và b là độ cao của mỗi ngọn núi, và c là độ dài của cáp treo.
     c² = a² + b² thay số vào ta được c² = 300² + 400²
     c² = 90000 + 160000 = 250000
     c = √250000 = 500 m

     Do đó, độ dài của cáp treo là khoảng 500 mét.
    Định lý Pythagoras là một trong những định lý cơ bản của toán học, đã được sử dụng trong hàng trăm năm và vẫn đóng vai trò quan trọng trong giáo dục toán học hiện nay. Nó không chỉ là một công cụ hữu ích để giải quyết các bài toán trong toán học, mà còn được áp dụng rộng rãi trong thực tiễn, từ kiến trúc đến khoa học vật lý.Nó là một trong những định lý đơn giản nhưng rất quan trọng của toán học, đóng vai trò quan trọng trong sự phát triển của toán học và khoa học vật lý.

   Trên đây là các thông tin giải đáp cho câu hỏi ? Định lý Pytago là gì? Công thức định lý Pytago? Định lý Pytago và ví dụ minh hoạ? Một số bài tập vận dụng liên quan đến định lý Pytago?... Để cập nhât các thông tin liên quan hoặc các thông tin mới nhất các bạn hãy liên hệ với chúng tôi.

     Liên hệ: 1900633720

     Bài viết tham khảo: Từ láy là gì?